Question

Please help thank you very much!

Answer 1

Hello!

Lets consider what the question asks for:

--> graphs of either line intersecting/parallel/identical

--> # of solutions the system has

The information given:

6x + y = 25

x + 3y = 3

Let's solve the FIRST problem

--> graphs of either line intersecting/parallel/identical

--> let's put both equations into slope-intercept form, where we

isolate the y-variable all by itself to one side

`6x+3y=25\\3y=-6x+25\\\\y=-2x+(25)/(3)`

`x+3y=3\\3y=-x+3\\y=-(1)/(3)x+1`

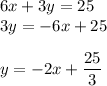
--> both equations AREN'T parallel as the slope (coefficient of x-

variable) aren't equal

--> both equations AREN'T identical as they don't look the same

--> both equations ARE INTERSECTING as they have different

slopes and aren't identical

Let's solve our second question:

--> how many solutions does the system have:

--> both lines intersect

-->both lines are linear as the highest power that the x-variable

has are 1

--> thus there is only ONE SOLUTION

Answer:

Intersecting

Has ONE SOLUTION