Question

Need answers asap!!! Pls and thank you!

Answer 1

1) ≈ 0,11 A

2) 224 V

3) I added a photo of my drawing

4) ≈ 8,34 Ω

5) ≈ 0,94 A

6) ≈ 0,35 A

7) 0,94 A

Step-by-step explanation:

1) Given:

R = 80 Ω

V = 9V

Find: I - ?

`i = (v)/(r) = (9)/(80) ≈ 0.11`

.

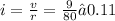
2) Given:

I = 2 A

R1 = 100 Ω

R2 = 12 Ω

Find: V - ?

This circuit is connected in series

R = R1 + R2

R = 100 + 12 = 112 Ω

V = I × R

V = 2 × 112 = 224 V

.

3) I added a photo of my drawing

4) Given:

R1 = R2 = R3 = 82 Ω

R4 = 12 Ω

V = 9 V

Find: R (total) - ?

This circuit is connected in parallel

`(1)/(r) = (1)/(r1) + (1)/(r2) + (1)/(r3) + (1)/(r4)`

Since R1 = R2 = R3, we can find the total resistance in these 3 resistors using this formula:

`r = (r1)/(n)`

n - the number of resistors

r1 - the resistance of one resistor (when all resistors have the same resistance)

`r(123) = (82)/(3) ≈ 27.33`

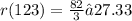
Now, let's find the remaining resistance:

`(1)/(r(total)) = (1)/(27.33) + (1)/(12) = (437)/(3644)`

`r(total) ≈8.34`

.

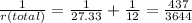
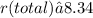
5) Given:

R1 = R2 = 50 Ω

R3 = 75 Ω

R4 = 45 Ω

V = 120V

Find: I - ?

R3 and R4 are connected in parallel

`(1)/(r(34)) = (1)/(75) + (1)/(45) = (8)/(225)`

`r(34) ≈28.13`

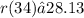
R1, R2 and R34 and conected in series

`r(total) = 28.13 + 50 + 50 = 128.13`

`i = (v)/(r) = (120)/(128.13) ≈0.94`

.

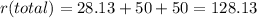
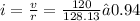
6) Given:

R3 = 75 Ω

Find: I3 - ?

First, we have to find the voltage across R3 and R4

In order to do that, first we have know what voltage is across R1 and R2 (since the resistance is these 2 resistors are the same, the voltage will also be the same):

V1 = V2 = I × R1 = 0,94 × 50 = 47 V

Then V4 = V5 (parallel conection) = 120 - 47 - 47 = 26 V

I3 = V3/R3 = 26/75 = 0,35 A

.

7) Given:

I (total) = 0,94 A

Find: I1, I2 - ?

I1 = I2 = 0,94 A, because the current in series connection stays the same in every part of the circuit