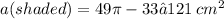Question

Learning Task 2 : Find the area of each shaded region. Assume that all angles that appear to be right triangle (3 points each).

Step by step answer
PLS

Answer 1

1. 60 ft^2

2. 175 cm^2

3. 36 cm^2

4. ≈ 121 cm^2

Explanation:

1.

First, let's find the area of the whole rectangle:

A (whole) = 7 × 12 = 84 ft^2

Then, we have to find the area of the smaller rectangle which is inside the whole rectangle:

A (smaller) = 3 × 8 = 24 ft^2

Finally, let's subtract the area of the smaller rectangle from the area of the whole rectangle and we'll get the answer:

A (shaded) = 84 - 24 = 60 ft^2

.

2.

The opposite side lengths of a rectangle are equal

First, we can find the shorter side's length of each shorter rectangle:

(16 - 9) / 2 = 3,5 cm

A shorter side of the larger rectangle would be:

16 - 9 = 7 cm

Now, we can find the area of two smaller rectangles that are on top of the larger one:

A (2 smaller rectangles) = 9 × 3,5 × 2 = 63 cm^2

Also, we have to find the area of the larger rectangle:

A (larger) = 16 × 7 = 112 cm^2

In order to find the area of the shaded region, we have to add both of these areas together:

A (shaded) = 63 + 112 = 175 cm^

.

3.

Given:

h = 12 cm

b (triangle's base) = 9 cm

a (rectangle's longer side) = 6 cm

c (rectangle's shorter side) = 3 cm

Find: A (shaded) - ?

First, let's find the area of the triangle:

`a(triangle) = (1)/(2) * b * h`

`a(triangle) = (1)/(2) * 9 * 12 = 54 \: {cm}^(2)`

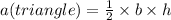
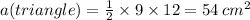
Now, we have to find the area of the rectangle:

`a(rectangle) = a * c = 6 * 3 = 18 \: {cm}^(2)`

In order to find the area of the shaded region, we have to subtract the rectangle's area from the triangle's area:

`a(shaded) = 54 - 18 = 36 \: {cm}^(2)`

.

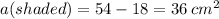
4.

Given:

r (radius) = 7 cm

a (rectangle's longer side) = 11 cm

b (rectangle's shorter side) = 3 cm

Find: A (shaded) - ?

First, let's find the area of the circle:

`a(circle) = \pi {r}^(2) = \pi * {7}^(2) = 49\pi \: {cm}^(2)`

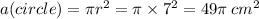
Now, we have to find the area of the rectangle:

`a(rectangle) = a * b = 11 * 3 = 33 \: {cm}^(2)`

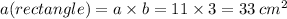
In order to find the shaded area, we have to subtract the rectangle's area from the circle's area:

`a(shaded) = 49\pi - 33 ≈ 121 \: {cm}^(2)`