Question

You have $20 to spend on taxi fare. The ride costs $5 plus $2.50 per

kilometer.
Write an inequality to determine the distance in kilometers, d, you can
ride for $20.
What is the maximum distance, in kilometers, you can ride for $20?
kilometers

Answer 1

In total you have $20.

Base fare of taxi is $5.

Per mile cost is $2.50.

Your total cost is where x is the number of miles. Since you're on a budget of maximum $20, the cost should be less than or equal to $20. We can write:

`5+2.5x\leq 20`

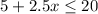
To find how many miles we can write, let's solve the inequality:

`5+2.5x\leq 20`

`2.5x\leq 20-5`

`2.5x\leq 15`

`x\leq (15)/(2.5)`

`x\leq 6`

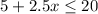
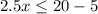
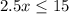
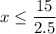
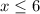
This means 6 is the maximum number of miles you can ride with $20.

ANSWER: Maximum 6 miles

Answer 2

To determine the distance in kilometers, d, you can ride for $20, we can use the following inequality: 5 + 2.5d ≤ 20 Simplifying the inequality, we get: 2.5d ≤ 15 d ≤ 6 Therefore, the maximum distance you can ride for $20 is 6 kilometers.