Question

A block is attached to two identical ideal springs. It is initially held so the whole setup is horizontal and the springs are not extended. The unextended length of each spring is 0.9 m with a spring constant of 473 N/m. The block is slowly lowered until the mass is in static equillibrium. The springs now make an angle θ = 20o with the horizontal as shown. What is the mass of the block? You may assume the block is a point mass (no volume).

Answer 1

`\blue{\huge {\mathrm{MASS \; OF \; THE \; BLOCK}}}`

`\\`

`{===========================================}`

`{\underline{\huge \mathbb{Q} {\large \mathrm {UESTION : }}}}`

• A block is attached to two identical ideal springs. It is initially held so the whole setup is horizontal and the springs are not extended. The unextended length of each spring is 0.9 m with a spring constant of 473 N/m. The block is slowly lowered until the mass is in static equillibrium. The springs now make an angle θ = 20° with the horizontal as shown. What is the mass of the block? You may assume the block is a point mass (no volume).

`{===========================================}`

`{\underline{\huge \mathbb{A} {\large \mathrm {NSWER : }}}}`

• The mass of the block is 1.9 kg.

`{===========================================}`

`{\underline{\huge \mathbb{S} {\large \mathrm {OLUTION : }}}}`

To solve for the mass of the block, we can use the forces acting on the block at equilibrium. We know that the force of gravity pulling down on the block is equal to the force of the springs pulling up.

The force of each spring can be found using Hooke's Law:

• 
  `\sf F = kx`

where:

• F is the force,
• k is the spring constant, and
• x is the displacement from the equilibrium position.

In this case, the displacement is equal to the extension of the spring, which is given by:

• 
  `\sf x = L(1-\cos\theta)`

where:

• L is the unextended length of the spring, and
• θ is the angle it makes with the horizontal.

So the force of each spring is:

• 
  `\sf F_(spring) = kx = kL(1-\cos\theta)`

At equilibrium, the forces in the vertical direction must balance, so we have:

• 
  `\sf 2F_(spring) = mg`

where

• m is the mass of the block and
• g is the acceleration due to gravity.

Substituting in the expression for
`\sf F_(spring)` and simplifying, we get:

`\sf\qquad\implies 2kL(1-\cos\theta) = mg`

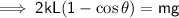
Solving for m, we obtain:

`\sf\qquad\implies m = (2kL(1-\cos\theta))/(g)`

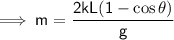
Plugging in the given values, we get:
`\\\begin{aligned}\sf m&=\sf (2(473\: N/m)(0.9\: m)[1-\cos(20^(\circ))][\sin(20^(\circ))])/((9.81 m/s^2))\\&=\boxed{\bold{\:1.9\: kg\:}}\end{aligned}`

Therefore, the mass of the block is 1.9 kg.

`{===========================================}`

`- \large\sf\copyright \: \large\tt{AriesLaveau}\large\qquad\qquad\qquad\qquad\qquad\qquad\tt 04/02/2023`

Answer 2

Approximately
`1.9\; {\rm kg}` (assuming that
`g = 9.81\; {\rm N\cdot kg^(-1)}`.)

Step-by-step explanation:

Let
`L = 0.9\; {\rm m}` denote the unextended length of each spring.

The length of each spring is now
`(L / \cos(\theta))`. The displacement of each spring would be
`x = L - (L / \cos(\theta)) = (1 - (1 / \cos(\theta)))\, L`.

The tension in each spring would be
`T = k\, x`, where
`k` is the spring constant.

Decompose the tension that each spring exerts on the block into two components:

• Horizontal:
  `T\, \cos(\theta)`.
• Vertical:
  `T\, \sin(\theta)`.

The two horizontal components balance each other since they are equal in magnitude. The two vertical components add on to each other to exert a total upward force of
`2\, T\, \sin(\theta)` on the block.

Since the block is in equilibrium, the resultant force on the block will be
`0`. The sum of these two (upward) vertical components of tension should balance the (downward) weight of the block:

`2\, T\, \sin(\theta) = m\, g`, where
`m` is the mass of the block.

Rearrange this equation to find the mass of the block:

`\begin{aligned} m &= (2\, T\, \sin(\theta))/(g) \\ &= (2\, k\, x\, \sin(\theta))/(g) \\ &= (2\, k\, L\, (1 - (1 / \cos(\theta))\, \sin(\theta))/(g) \\ &= (2\, (473)\, (0.9)\, (1 - (1 / \cos(20^(\circ))))\, \sin(20^(\circ)))/((9.81))\; {\rm kg} \\ &\approx 1.9\; {\rm kg}\end{aligned}`.