Question

The diagonals of a rhombus are 3.5 and 12. A circle is tangent to 2 sides (or their extensions) of the rhombus, and is centered at one of the vertices of the rhombus. Find the exact value of the circle area. (Make a drawing for all cases.) PLEASE HELP!!

Answer 1

11.2896π square units

Explanation:

A rhombus is a quadrilateral (a four-sided polygon) with sides of equal length. The diagonals of a rhombus bisect each other at right angles.

Let the vertices of the rhombus be A, B, C and D.

As the diagonals of rhombus ABCD are 3.5 and 12 units, then AC = 3.5 and BD = 12.

Place a circle centered at vertex C and tangent to sides AD and AB (refer to attachment 1).

The diagonals divide the rhombus into 4 congruent right triangles with legs measuring 1.75 units and 6 units.

Let the point of intersection of the two diagonals be M.

Use the tangent trigonometric ratio to find the measure of angle MAB in triangle AMB (refer to attachment 2).

`\begin{aligned} \tan (\theta)&=(\sf opposite \;side)/(\sf adjacent\;side)\\\\ \implies \tan (MAB)& =(6)/(1.75)\\\\&=(24)/(7)\\\\\angle MAB&=\arctan\left((24)/(7)\right)\end{aligned}`

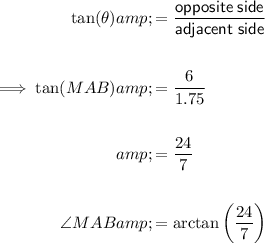
The tangent of a circle is perpendicular to its radius.

Therefore, the radius of the circle with center C is a straight line from point C perpendicular to line segment AB (labelled in green in attachment 3). The point of intersection of the radius and side AB is E.

By drawing the radius (CE), we have created another right triangle, AEC, where its hypotenuse is the shortest diagonal of the rhombus (AC), its longest leg is the radius (CE), and the angle opposite the radius is angle MAB.

Using this information and the sine trigonometric ratio, we can calculate length of the radius of circle C:

`\begin{aligned}\sin(\theta)&=\sf (opposite\;side)/(hypotenuse)\\\\\implies \sin\left(MAB\right)&=(CE)/(AC)\\\\\implies \sin\left(\arctan\left((24)/(7)\right)\right)&=(r)/(3.5)\\\\0.96&=(r)/(3.5)\\\\r&=3.36\; \sf units\end{aigned}`

Now we have calculated the exact radius of the circle, we can find its area by substituting the value of r into the area of a circle formula:

`\begin{aligned}\textsf{Area of a circle}&=\pi r^2\\&=\pi (3.36)^2\\&=11.2896 \pi\; \sf square \;units\end{aligned}`

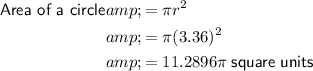
Therefore, the exact value of the circle area is 11.2896π square units.

Note: Attachment 4 is the circle centered at the other 3 vertices of the rhombus. All circles are congruent and therefore have the same area.