Question

Consider a circle whose equation is x2 + y2 – 2x – 8 = 0. Which statements are true? Select three options. The radius of the circle is 3 units. The center of the circle lies on the x-axis. The center of the circle lies on the y-axis. The standard form of the equation is (x – 1)² + y² = 3. The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.

Answer 1

• Correct options are A, B, E

--------------------------

Standard form for the equation of a circle is:

• (x − h)² + (y − k)² = r², where (h, k) is the center and r is the radius

Convert the given equation into standard form:

• x² + y² - 2x - 8 = 0
• x² - 2x + 1 + y² - 9 = 0
• (x - 1)² + y² = 9
• (x - 1)² + y² = 3²

Its center is ( 1, 0) and radius is r = 3.

Let's verify the statements:

• A) The radius of the circle is 3 units - TRUE, r = 3;
• B) The center of the circle lies on the x-axis - TRUE, point (1, 0) is on the x-axis;
• C) The center of the circle lies on the y-axis - FALSE, the x- coordinate of the center is not zero;
• D) The standard form of the equation is (x – 1)² + y² = 3 - FALSE, r²= 9 but not 3;
• E) The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9, TRUE, its radius is r² = 9 ⇒ r = 3.

Answer 2

See below

Explanation:

To find:-

• Which statements are true .

Answer:-

The given equation of the circle is ,

`\longrightarrow x^2+y^2-2x-8 = 0 \\`

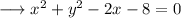
For finding the correct statements , we need to convert this equation into standard form for a circle.

The standard equation of circle is given by,

`\boxed{\begin{tabular}{c}\textbf{\underline{ \red{Standard\ equation\ of \ circle }}} \\ \\ \text{ The standard equation of a circle is given by:-} \\\\ \longrightarrow \underline{\underline{ (x-h)^2+(y-k)^2 = r {}^(2)}} \\\\ \text{where} , \\\\ \bullet\text{ (h,k) is the centre of the circle.}\\\\\bullet\text{`

Now for that we need to complete the square for "x" . This can be done by ,

Rearrange the terms,

`\longrightarrow x^2-2x + y^2-8 = 0 \\`

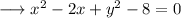
Add and subtract 1² .

`\longrightarrow ( x^2 -2x +1^2 ) - 1^2 + y^2-8=0 \\`

Simplify,

`\longrightarrow (x^2-2(1)x+1^2) - 1-8 + y^2=0 \\`

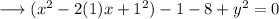
Notice that the terms inside the small brackets are in the form of a² - 2ab + b² , which is the whole square of (a-b) . So we can write it as,

`\longrightarrow (x-1)^2 +y^2 - 9 = 0 \\`

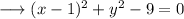
Add 9 on both the sides ,

`\longrightarrow (x-1)^2 + y^2 = 9\\`

This can be written as,

`\longrightarrow \underline{\underline{ \boldsymbol{(x-1)^2+(y-0)^2 = 3^2}}} \\`

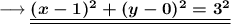
On comparing it to the standard form, we have;

`\longrightarrow\boxed{ \text{Center = (1,0) }} \\`

`\longrightarrow\boxed{ \text{ Radius = 3 \ units}} \\`

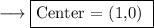
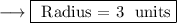
Let's check the given statements ,

Statement 1: The radius of the circle is 3 units.

• This statement is true as we just calculated the radius to be 3 units.

Statement 2: The centre of the circle lies on the x-axis.

• This statement is also true as you can see that the y coordinate to the centre is 0 , and the x coordinate is 1 , so it will be on x-axis .

Statement 3: The statement of the circle lies on the y-axis.

• This statement is false since in the previous statement we proved that the centre lies on the x-axis .

Statement 4: The standard equation of the circle is (x-1)²+y² = 3

• This statement is false as we calculated the value of r² to be 9 .

Statement 5: The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.

• The given equation of circle is x² + y² = 9 , if we convert this into standard form, we will get ; x² + y² = 3² . Now on comparing it to the standard equation, we see that the radius is 3 units . Hence the given statement is also true .

The graph for the same has been attached.