Question

Solve for
`y` as a function of
`x`:


`y^\prime-xe^y=2e^y` and
`y(0)=0`

Answer 1

`y=-ln(-(x^2)/(2)-2x+1)`

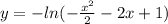
see images for steps.

ask for explanation.

hope this helps,

jeron

:)

takeaways:

remember that y' is dy/dx

separable differentiation (when you get the side with y with its dy and the side with x with its dx... only possible when multiplying or dividing NO ADDITION OR SUBTRACTION)


key terms:

separable differentiation (when you get the side with y with its dy and the side with x with its dx... only possible when multiplying or dividing NO ADDITION OR SUBTRACTION)
initial condition (a point on the graph of y)
general solution (involves the +c)
particular solution (you used initial condition to find the c)