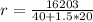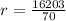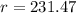Answer:
His rate is a whopping $231.47 per hour.
:)
Explanation:
We can conclude that.
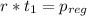 is the gross pay from his regular hours.
is the gross pay from his regular hours.
 is the gross pay from his overtime hours.
is the gross pay from his overtime hours.
So all together we can say
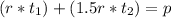
We are looking for his hourly rate.
Lets solve for
 .
.
Multiply the terms in the parenthesis.
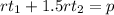
Factor
 out of
out of
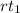 .
.

Factor
 out of
out of
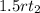 .
.
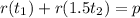
Factor
 out of
out of
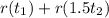 .
.
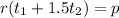
Divide each term in
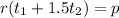 by
by
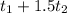 and simplify.
and simplify.
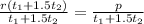
Simplify the left side. Cancel the common factor of
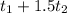
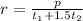
Now we have an equation to find his regular hourly rate.
We are given
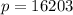
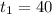
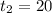
Lets plug these numbers into our equation for
 .
.