Question

What is the surface

area of a pyramid
with a square base
with sides of 10
inches and a length of
15 inches?

Answer 1

To find the surface area of a pyramid with a square base, we need to find the area of the square base and the area of each triangular face, then add them together.

The area of the square base is the square of the length of one of its sides. In this case, the side length is 10 inches, so the area of the base is:

`\rm A_(base) = 10^2 = 100 \text{ square inches}`

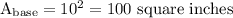
To find the area of each triangular face, we need to find the height of the pyramid. The height of the pyramid is the perpendicular distance from the apex (the top of the pyramid) to the base. To find the height, we can use the Pythagorean theorem, since we know the length of the slant height (15 inches) and half the length of the base (5 inches):

`\rm{h = √(15^2 - 5^2) = √(200) = 10√(2) \text{ inches}}`

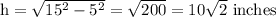
Now we can find the area of each triangular face using the formula:

`\rm{A_(face) = (1)/(2) * \text{base} * \text{height}}`

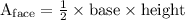
where the base is the side length of the square base, and the height is the height of the pyramid. In this case, we have:

`\rm{A_(face) = (1)/(2) * (10 \text{ inches}) * (10√(2) \text{ inches}) = 50√(2) \text{ square inches}}`

Finally, we can find the surface area of the pyramid by adding the area of the base and the area of the four triangular faces:

`\rm{A_(total) = A_(base) + 4A_(face) = 100\text{ square inches} + 4(50√(2) \text{ square inches}) \approx 314.16 \text{ square inches}}`

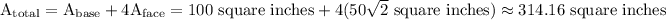
Therefore, the surface area of the pyramid is approximately 314.16 square inches.