Question

If zeros of the polynomial x²+ 4x + 2a are alpha and 2/alpha then find the value of a

Answer 1

Explanation:

Answer 2

a = 1

Explanation:

The zeros of a polynomial P(x) are the x-values that make the polynomial equal to zero, P(x) = 0.

The sum of the zeros of a quadratic equation ax² + bx + c = 0 is -b/a.

The product of the zeros of a quadratic equation ax² + bx + c = 0 is c/a.

Given polynomial:

`x^2+ 4x + 2a`

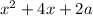
Therefore, the zeros of the given polynomial are the x-values that make x²+ 4x + 2a = 0.

Comparing the given polynomial with ax² + bx + c = 0:

• a = 1
• b = 4
• c = 2a

If the zeros of the polynomial x²+ 4x + 2a are α and α/2, then using the zeros product formula:

`\begin{aligned}\alpha \cdot (2)/(\alpha) &= (c)/(a) \\\\\implies 2&= (2a)/(1)\\\\\implies 2&=2a\\\\\implies (2)/(2)&=a\\\\\implies a&=1\end{aligned}`

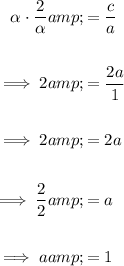
Therefore, the value of a is 1.