Question

The volume of a cone is 72 pie, the height is 6cm, what is the radius of the base of the cone

Answer 1

r≈3.39

Explanation:

I'm not quite sure but it's the best I can do.

Answer 2

radius of base = 6 cm

Explanation:

In order to calculate the radius of the base of a cone given its volume and height, we have to use the formula for the volume of a cone:

`\boxed{\mathrm{V = (1)/(3) \pi r^2h}}`,

where:

• V ⇒ volume of the cone

• r ⇒ radius of the base of the cone

• h ⇒ height of the cone

The question gives us the value of the volume of the cone (72π cm³) as well as its height (6 cm). By substituting these values into the equation above, we can solve for r to get the radius of the base of the cone:

`\mathrm{V = (1)/(3) \pi r^2h}`

⇒
`72 \pi = (1)/(3) * \pi * r^2 * 6`

⇒
`r^2 = (72 \pi)/(2 \pi)`

⇒
`r = \sqrt{(72 \pi)/(2 \pi)}`

⇒
`r = √(36)`

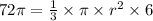
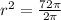
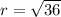
⇒ r = 6 cm

Therefore, the radius of the base of the cone is 6 cm.