Answer:

Explanation:
Given equation:
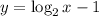
To fill out the given x-y chart, substitute each given value of x into the given log equation.
The argument of a log function can only take positive arguments, so when x = -2, x = -1 and x = 0, the y-values are undefined.
The values of y for x = 1 and x = 2 are:
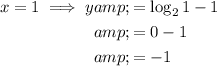
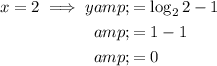
Therefore, the completed x-y chart for the equation y = log₂x - 1 is:

Note: I have used DNE for does not exist.