Question

PLEASE HELP!! AND EXPLAIN

6. What is the area of this figure?

Answer 1

D. 60cm2
Solution: 48+12=60

Answer 2

60 cm²

Explanation:

We can split this figure into two simpler polygons (a triangle and rectangle), solve for the area of each one, then add their areas together to get the total area of the figure.

Step 1: Rectangle

The easiest shape to recognize is the large rectangle in the lower half of the figure. We can find its area using the formula:

`A = l \cdot w`,

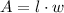where
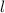`l` is the rectangle's length and
`w` is its width.

`A = 12 \text{ cm} \cdot 4\text{ cm}`

`A = 48 \text{ cm}^2`

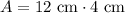
So, the area of the rectangle is 48 cm².

Step 2: Triangle

We can see there is a triangle in the top half of the figure. The area of a triangle is defined as:

`A = (1)/(2) \cdot b \cdot h`,

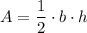where
`b` is the length of the triangle's base and
`h` is its height.

The trick here is to find out the triangle's base and height measurements.

We can solve for the height by subtracting the height of the bottom half (height of the rectangle) from the total height.

`h = 8 \text{ cm} - 4 \text{ cm}`

`h = 4 \text{ cm}`

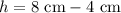
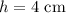
We can solve for the width by subtracting the lengths next to the triangle from the total width of the figure.

`w = 12 \text{ cm} - 3\text{ cm} - 3\text{ cm}`

`w = 6 \text{ cm}^2`

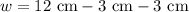
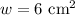
Now, we can plug these values into the area formula:

`A = (1)/(2) \cdot 6\text{ cm} \cdot 4\text{ cm}`

`A = 3\text{ cm} \cdot 4\text{ cm}`

`A = 12\text{ cm}^2`

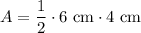
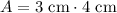
So, the area of the triangle is 12 cm².

Step 3: Total Area

Finally, we can solve for the total area of the figure by adding the area of the rectangle and the area of the triangle.

`A = 48 \text{ cm}^2 + 12\text{ cm}^2`

`\boxed{A = 60\text{ cm}^2}`

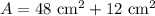
The total area of the figure is 60 cm².