Answer:
C) 53.3%
The probability that a data value is between 206 and 230
P( 206 ≤X≤230) = 0.5328 = 53.3%
Explanation:
Explanation
Given that Mean of the Normal distribution(μ) = 222
Given that the standard deviation of the Normal distribution (σ) = 16
Let 'X' be the random variable in the Normal distribution
we have to find that the probability that a data value is between 206 and 230
solution:-
Step(i):-
Let 'X' = 206
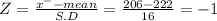
Let X = 230
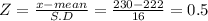
Step(ii):-
The probability that a data value is between 206 and 230
P( 206 ≤X≤230) = P( -1≤Z≤0.5)
= |A(0.5)+A(-1)|
= 0.1915+0.3413
= 0.5328
final answer:-
The probability that a data value is between 206 and 230
P( 206 ≤X≤230) = 0.5328 = 53.3%