Question

Rhombus JKLM with vertices J(-10, 2), K(-2, 8), L(6,2), and M(-2, -4): k = ¹/2​

Answer 1

Sorry I have no clue hope u find ur answer I need points i a mf failing and everything is due today

Answer 2

The new coordinates after the dilation will be
`\( J'(-5, 1) \), \( K'(-1, 4) \), \( L'(3, 1) \), and \( M'(-1, -2) \).`

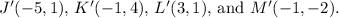
To find the new coordinates of a figure after a dilation, we multiply the original coordinates by the scale factor. Given that the scale factor k is
`\( (1)/(2) \)`, the new coordinates (x', y') for each vertex (x, y) of the rhombus can be found using the following equations:

`\[ x' = x * k \]\[ y' = y * k \]`

Now we'll apply this to each vertex of the rhombus J(-10, 2), K(-2, 8), L(6, 2), and M(-2, -4) with the given scale factor
`\( k = (1)/(2) \):`

1. For vertex J(-10, 2):

`\[ J'(x') = -10 * (1)/(2) = -5 \]\[ J'(y') = 2 * (1)/(2) = 1 \]`

So J' will be (-5, 1)

2. For vertex K(-2, 8):

`\[ K'(x') = -2 * (1)/(2) = -1 \]\[ K'(y') = 8 * (1)/(2) = 4 \]`

So K' will be (-1, 4) .

3. For vertex L(6, 2):

`\[ L'(x') = 6 * (1)/(2) = 3 \]\[ L'(y') = 2 * (1)/(2) = 1 \]`

So L' will be (3, 1) .

4. For vertex M(-2, -4):

`\[ M'(x') = -2 * (1)/(2) = -1 \]\[ M'(y') = -4 * (1)/(2) = -2 \]`

So M' will be (-1, -2) .