Polynomial expressions of
 degree with one unknown (only
degree with one unknown (only
 ) have
) have
 roots. We use the formula below to determine these roots;
roots. We use the formula below to determine these roots;
This formula is valid for equations of the form
 . We can convert the equation given in the question into this format to get the result;
. We can convert the equation given in the question into this format to get the result;
Hence, the value of
 :
:
 ,
,
the value of
 :
:
 ,
,
the value of
 :
:
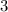 .
.
Now, we can find the roots of this equation by using this formula;