Answer:
Approximately
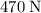 .
.
(Assuming that
 and that air resistance is negligible.)
and that air resistance is negligible.)
Step-by-step explanation:
Under the assumptions, the acceleration of the child would be constantly
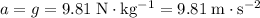 while the child was in the air.
while the child was in the air.
Apply the SUVAT equation
 to find the velocity
to find the velocity
 of the child right before landing:
of the child right before landing:
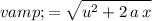 , where:
, where:
 is the initial velocity of the child,
is the initial velocity of the child,
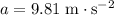 is the vertical acceleration, and
is the vertical acceleration, and
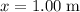 is the vertical displacement (change in height.)
is the vertical displacement (change in height.)
The child is at rest
 after contact. During that
after contact. During that
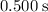 , velocity would have changed by
, velocity would have changed by
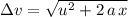 . Momentum of the child would have changed by
. Momentum of the child would have changed by
 , where
, where
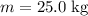 is the mass of the child.
is the mass of the child.
Divide this change in momentum by the duration
 to find the average net force:
to find the average net force:
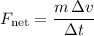 .
.
There are two forces on the child: upward normal force from the ground
 and downward gravitational attraction
and downward gravitational attraction
 from the Earth. The resultant force on the child points upwards:
from the Earth. The resultant force on the child points upwards:
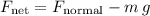 .
.
Rearrange this equation to find the normal force on the child:
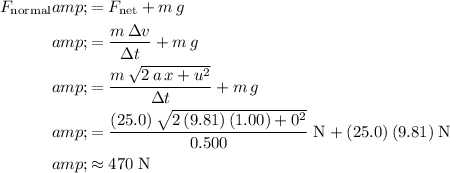 .
.
This normal force from the ground on the child is the reaction to the force that the child exerted on the ground. The two forces will have the same magnitude: approximately
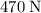 . Hence, the child would have exerted an average force of approximately
. Hence, the child would have exerted an average force of approximately
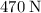 on the ground during that
on the ground during that
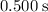 .
.