Question

At 250 °C a gas has a volume of 425 mL. What is the volume of this gas at 125°C?

Answer 1

Charles's Law-

`\:\:\:\:\:\: \:\:\:\:\:\:\star\longrightarrow\sf \underline{(V_1)/(T_1)=(V_2)/(T_2)}\\`

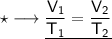
Where:-

• V₁ = Initial volume
• T₁ = Initial temperature
• V₂ = Final volume
• T₂ = Final temperature

As per question, we are given that -

• V₁=425 mL
• T₁ = 250°C
• T₂ =125°C

We are given the initial temperature and the final temperature in °C.So, we first have to convert those temperatures in Celsius to kelvin by adding 273-

`\:\:\:\:\:\:\star\sf T_1` = 250+ 273 = 523 K

`\:\:\:\:\:\:\star\sf T_2` =125+273 = 398K

Now that we have obtained all the required values, so we can put them into the formula and solve for V₂ :-

`\:\:\:\:\:\: \:\:\:\:\:\:\star\longrightarrow\sf \underline{(V_1)/(T_1)=(V_2)/(T_2)}\\`

`\:\:\:\:\:\:\:\:\:\:\:\:\longrightarrow \sf V_2= (V_1)/(T_1)* T_2\\`

`\:\:\:\:\:\:\:\:\:\:\:\:\longrightarrow \sf V_2= (425)/(523)* 398\\`

`\:\:\:\:\:\:\:\:\:\:\:\:\longrightarrow \sf V_2= 0.8126195..........* 398\\`

`\:\:\:\:\:\: \:\:\:\:\:\:\longrightarrow \sf V_2 =323.4225.............\\`

`\:\:\:\:\:\:\:\:\:\:\:\:\longrightarrow \sf\underline{ V_2= 323.42\:mL}\\`

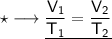
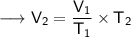
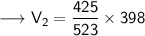
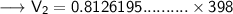
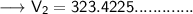
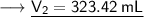
Therefore, the volume of this gas at 125°C will become 323.42 mL.