Question

PLEASE ANSWER!!!!!

Weekly wages at a certain factory are normally distributed with a mean of $400 and a standard deviation of $50. Find the probability that a worker selected at random makes between $400 and $550

Answer 1

49.87%

Explanation:

We know the following information:

$400 is the average weekly wage

$50 is the standard deviation (from the average wage)

To solve for the probability that a randomly-selected worker makes between $400-550, we have to solve for the standard score of each end of the range.

First, the standard score (Z) of $400:

`Z = \frac{\text{value}-\text{average}}{\text{std deviation}}`

`Z_(400) = (400-400)/(50) = 0`

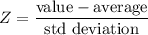
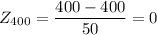
The standard score of $400 is 0, since it is the average (mean) wage.

Second, the standard score of $550:

`Z_(550) = (550-400)/(50) = 3`

The standard score of $550 is 3.

The probability that a worker's weekly wage is between $400 and $550 is equal to the probability that the standard score is between 0 and 3.

So, we can plug the standard scores that we just solved for into a distribution calculator to determine both probabilities.

P(0 < Z < 3) ≈ 49.87%