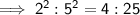Question

Sam has a deck that is shaped like a triangle with a base of 18 feet and a height of 7 feet. He plans to build a 2:5 scaled version of the deck next to his horse’s water trough.

Part A: What are the dimensions of the new deck, in feet? Show every step of your work.

Part B: What is the area of the original deck and the new deck, in square feet? Show every step of your work.

Part C: Compare the ratio of the area to the scale factor. Show every step of your work.

Answer 1

A) The dimensions of the new triangular deck are:

• base = 45 feet
• height = 17.5 feet

B) Area of original deck = 63 square feet
Area of new deck = 393.75 square feet

C) The ratio of the area is 4 : 25. This is the square of the scale factor.

Explanation:

Part A

The given scale is 2 : 5. This means that the ratio of the measurements of the corresponding sides of two objects is 2 to 5. In other words, if one object has a length of 2 units, the corresponding length of the other object is 5 units. So in this scenario, a 2 : 5 scaled version means that for every 2 foot of the original deck, there is 5 foot of the new deck.

Therefore, if the original base of the triangle is 18 feet, the new base, b, will be:

`\implies \sf 2 : 5 = 18 : b`

`\implies \sf (2)/(5) = (18)/(b)`

`\implies \sf 2 \cdot b=18 \cdot 5`

`\implies \sf b=(18 \cdot 5)/(2)`

`\implies \sf b=45\;ft`

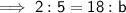
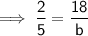
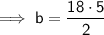
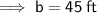
Similarly, if the original height of the triangle is 7 feet, the new height, h, will be:

`\implies \sf 2 : 5 = 7 : h`

`\implies \sf (2)/(5) = (7)/(h)`

`\implies \sf 2 \cdot h=7 \cdot 5`

`\implies \sf h=(7\cdot 5)/(2)`

`\implies \sf h=17.5\;ft`

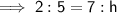
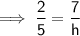
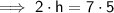
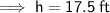
Therefore, the dimensions of the new triangular deck are:

• base = 45 feet
• height = 17.5 feet

`\hrulefill`

Part B

The area of a triangle is half of the product of its base and height:

`\boxed{\sf A=(1)/(2)bh}`

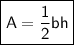
Area of the original deck:

`\implies \sf A=(1)/(2) \cdot 18 \cdot 7`

`\implies \sf A=9 \cdot 7`

`\implies \sf A=63\;ft^2`

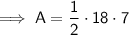
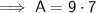
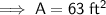
Area of the new deck:

`\implies \sf A=(1)/(2) \cdot 45\cdot 17.5`

`\implies \sf A=22.5 \cdot 17.5`

`\implies \sf A=393.75\;ft^2`

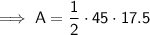
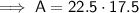
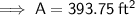
Therefore, the areas of the two decks are:

• Area of original deck = 63 square feet
• Area of new deck = 393.75 square feet

`\hrulefill`

Part C

The ratio of the area of the original deck to the area of the new deck is:

`\implies \textsf{Area original deck}:\textsf{Area new deck}=\sf 63 : 393.75`

To rewrite the ratio in its simplest form, multiply both sides of the ratio by 16:

`\implies \sf 63 \cdot 16: 393.75 \cdot 16=1008 :6300`

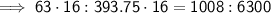
Then divide both sides of the ratio by 252:

`\implies \sf (1008)/(252):(6300)/(252)=4:25`

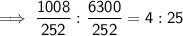
Therefore, the ratio of the area of the original deck to the area of the new deck in its simplest terms is 4 : 25.

If we compare this to the original scale factor 2 : 5 (which is the ratio of length), we can see that the ratio of area is the square of the scale factor:

`\implies \sf 2^2:5^2=4:25`