Question

Distance between (1,5) and (-6,-2)

Answer 1

`\:\: \:\: \:\star` We are asked to find out the distance between (1,5) and (-6,-2).We know the formula to find the distance between two points is given by -

`\:\: \star \underline{ \sf{ Distance = √( (y_2 -y_1)^2 + (x_2-x_1)^2)}}\\`

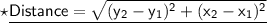
As per question, points are -

• A (1,5)

• B(-6,-2)

Now that we are given the points, so we can put them into the formula and solve for distance between them.Which is -

`\:\: \:\: \:\star \underline{ \sf{ Distance = √( (y_2 -y_1)^2 + (x_2-x_1)^2)}}\\`

`\longrightarrow \sf Distance_((AB)) = √( (-2-5)^2 + (-6-1)^2 )\\`

`\:\:\:\:\:\longrightarrow \sf Distance_((AB))= √( (-7)^2 + (-7)^2 )\\`

`\:\:\:\:\longrightarrow \sf Distance_((AB)) = √( 49+49 )\\`

`\: \:\:\:\: \:\longrightarrow \sf Distance _((AB))= √( 98)\\`

`\: \:\:\: \:\longrightarrow \sf Distance_((AB)) = √(49 * 2)\\`

`\:\: \:\: \:\:\longrightarrow \sf\underline{ Distance_((AB)) = 7√2}\\`

`\: \:\:\: \:\:\longrightarrow \sf Distance_((AB) )= 9.89949......\\`

`\: \:\:\: \:\:\longrightarrow \sf \underline{Distance_((AB) )= 9.9\:(Approx)}\\`

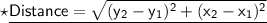
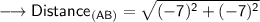
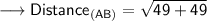
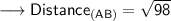
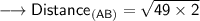
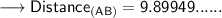
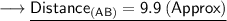
Therefore, the distance between (1,5) and (-6,-2) is 7√2 or, 9.9 ( Approx).