Question

HEEEEEEEELLLLLLLLLLPPPPPPPPP!!!!!!!!!

Answer 1

The horizontal translation of the function is 3 units to the right (from the parent function). Therefore, we subtract 3 from the x-value of the function.

The equation of the graphed function in vertex form is:

`\boxed{y = (x - 3)^2- 2}`

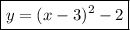
Explanation:

The given graph shows a parabola that opens upwards.

Therefore, the equation for this function is a quadratic equation with a positive leading coefficient.

The vertex of a parabola is the minimum point of a parabola that opens upwards, or the maximum point of a parabola that opens downwards.

From inspection of the given graph, the vertex of the function is (3, -2).

The parent function of a parabola that opens upwards is y = x². This has a vertex at (0, 0).

Therefore, given the vertex of the given function is (3, -2), the parent function has been translated 3 units right and 2 units down.

For a horizontal translation to the right, we subtract the number of units from the x-value of the function.

For a vertical translation down, we subtract the number of units from the function.

Therefore, a translation of 3 units right and 2 units down from the parent function y = x² is:

`\boxed{y = (x - 3)^2- 2}`

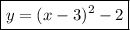
This function is written in vertex form.

To write the equation in standard form, expand the brackets and simplify:

`\implies y=(x-3)(x-3)-2`

`\implies y=x^2-3x-3x+9-2`

`\implies y=x^2-6x+7`

`\hrulefill`

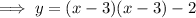
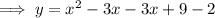
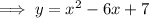
Additional comments

The vertex form of a quadratic equation is y = a(x - h)² + k, where (h, k) is the vertex. Therefore, the "k" value refers to the y-value, which is the vertical translation from the parent function.

As your question refers to the "k" value for the horizontal translation, we assume that it is not referring to the k-value of the vertex form.