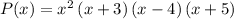Question

2. Use the Factor Theorem to determine if (x-4) is a factor of the polynomial function

P(x) = x5 + 4x4 - 17x³ - 60x²
Clearly state that (x-4) is a factor, or that (x-4) is not a factor. Show all work.

Answer 1

Yes, (x - 4) is a factor of polynomial function P(x) = x⁵ + 4x⁴ - 17x³ - 60x².

Explanation:

The Factor Theorem states that if f(x) is a polynomial, and f(a) = 0, then (x - a) is a factor of f(x).

Therefore, according to the Factor Theorem, if (x - 4) is a factor of P(x) then P(4) = 0.

To determine if (x - 4) is a factor of P(x), substitute x = 4 into the function and solve.

`\begin{aligned}x=4 \implies P(4)&=(4)^5+4(4)^4-17(4)^3-60(4)^2\\&=1024+4(256)-17(64)-60(16)\\&=1024+1024-1088-960\\&=2048-1088-960\\&=960-960\\&=0\end{aligned}`

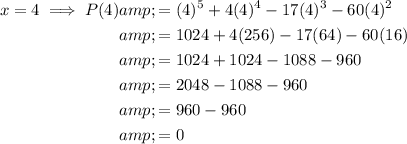
As P(4) = 0, this confirms that (x - 4) is a factor of polynomial function P(x) = x⁵ + 4x⁴ - 17x³ - 60x².

`\hrulefill`

Additional comments

The fully factored form of the given polynomial function is:

`P(x)=x^2\left(x+3\right)\left(x-4\right)\left(x+5\right)`