Question

A submarine is passing by a solar station, located al (0,0), that can detect objects that

are as far away as 5km in any direction. A swiss submarine is traveling along a trajectory defined by y= -2/3x +26/3 where x and y represent distances measured in kilometers. Determine algebraically whether the sonar station will detect the submitline.​

Answer 1

The sonar station will not detect the submarine.

Explanation:

The area that the sonar station can detect can be modelled as a circle with center (0, 0) and radius 5 km.

The equation of a circle formula is (x - h)² + (y - k)² = r², where (h, k) is the center and r is the radius.

Therefore, the equation of the circle modelling the perimeter of the sonar station detection area is:

`\implies (x-0)^2+(y-0)^2=5^2`

`\implies x^2+y^2=25`

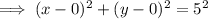
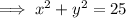
To determine whether the sonar station will detect a swiss submarine traveling along a trajectory defined by y = -2/3x + 26/3, substitute the equation of the trajectory into the found equation of the circle.

`\implies x^2+\left(-(2)/(3)x+(26)/(3)\right)^2=25`

Simplify:

`\implies x^2+(4)/(9)x^2-(104)/(9)x+(676)/(9)=25`

`\implies 9x^2+4x^2-104x+676=225`

`\implies 13x^2-104x+451=0`

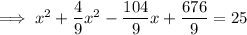
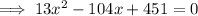
Solve the equation for x using the quadratic formula:

`x=(-b \pm √(b^2-4ac))/(2a)\quad\textsf{when }\:ax^2+bx+c=0`

`\implies x=(-(-104) \pm √((-104)^2-4(13)(451)))/(2(13))`

`\implies x=(104 \pm √(-12636))/(26)`

`\implies x=(104 \pm 18√(39)\:i)/(26)`

`\implies x=4 \pm (9√(39))/(13)\:i`

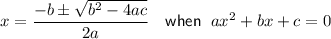
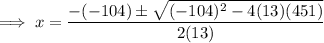
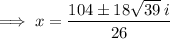
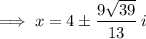
As the solutions are complex numbers, this means that the linear trajectory of the submarine will not intersect the detection area of the sonar station. Therefore, the sonar station will not detect the submarine.