Question

1) How many moles of gas occupy 58 L at a pressure of 1.55 atmospheres and a temperature of 222 K?

Answer 1

To find the moles of the gas , we can use the ideal gas law. Which states -

`\:\:\:\:\:\:\:\:\:\star\longrightarrow \sf \underline{PV=nRT} \\`

Where:-

• P is the pressure measured in atmospheres
• V is the volume measured in liters
• n is the number of moles.
• R is the ideal gas constant (0.0821 L atm mol⁻¹ K⁻¹).
• T is the temperature measured in kelvin.

As per question, we are given that-

• P=1.55 atm
• V= 58 L
• T = 222 K
• R = 0.08206 L atm mol⁻¹ K⁻¹

Now that we have all the required values, so we can put them all in the Ideal gas law formula and solve for moles -

`\:\:\:\:\:\:\:\:\:\star\longrightarrow \sf \underline{PV=nRT} \\`

`\:\:\:\:\:\:\:\:\:\longrightarrow \sf 1.55 * 58 = n * 0.0821 * 222\\`

`\:\:\:\:\:\:\:\:\:\longrightarrow \sf 89.9 = n * 18.2262\\`

`\:\:\:\:\:\:\:\:\:\longrightarrow \sf n * 18.2262 =89.9\\`

`\:\:\:\:\:\:\:\:\:\:\:\:\longrightarrow \sf n = (89.9)/(18.2262)\\`

`\:\:\:\:\:\:\:\:\:\:\:\:\longrightarrow \sf n =4.9324......\\`

`\:\:\:\:\:\: \:\:\:\:\:\:\longrightarrow \sf \underline{n =4.93 \:moles }\\`

Therefore, 4.93 moles of gas will be occupied 58 L at a pressure of 1.55 atmospheres and a temperature of 222K.

Answer 2

4.93 moles

Step-by-step explanation:

To find how many moles of gas pressure occupy 58 L at a pressure of 1.55 atmospheres and a temperature of 222 K, use the ideal gas law.

Ideal Gas Law

`\boxed{\sf PV=nRT}`

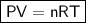
where:

• P is the pressure measured in atmospheres (atm).
• V is the volume measured in liters (L).
• n is the number of moles.
• R is the ideal gas constant (0.08206 L atm mol⁻¹ K⁻¹).
• T is the temperature measured in kelvin (K).

As we are solving for the number of moles, rearrange the equation to isolate n:

`\implies \sf n=(PV)/(RT)`

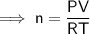
Given values:

• P = 1.55 atm
• V = 58 L
• R = 0.08206 L atm mol⁻¹ K⁻¹
• T = 222 K

Substitute the values into the formula and solve for n:

`\implies \sf n=(1.55 \cdot 58)/(0.08206 \cdot 222)`

`\implies \sf n=(89.9)/(18.21732)`

`\implies \sf n=4.93\;mol\; (3\;s.f.)`

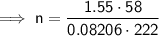
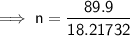
Therefore, 4.93 moles of gas occupy a volume of 58 L at a pressure of 1.55 atm and a temperature of 222 K.