Question

A company finds it can produce 30 heaters for $7500 while producing 40 heaters cost $9000, express the cost y as a linear function of the number of heaters x

express the cost y as a a linear function of the numbers of heatrs x

Answer 1

y = 150x + 3000

Explanation:

We can express the cost (y) as a linear function of heater quantity (x) by writing the equation in the slope-intercept form (y = mx + b), where m is the slope (in this case change in cost / change in heater quantity) and b is the y-intercept (when x = 0).

To find the slope (m), we can use the slope formula, which is

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) )`, where x1 and y1 are one point and x2 and y2 are the other point.

If we allow (30, 7500) to represent x1 and y1 and (40, 9000) to represent x2 and y2, our slope is:

`m=(9000-7500)/(40-30)\\ \\m=(1500)/(10)\\ \\m=150`

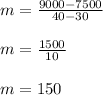
Now, we can find the y-intercept by plugging in the slope and one of the points and solving for b:

`7500=150(30)+b\\7500=4500+b\\3000=b`

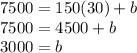
Thus, our equation where y (cost) is a function of x (heater quantity) is y = 150x + 3000