-------------------------------------------------------------------------------------------------------------
Answer:

-------------------------------------------------------------------------------------------------------------
Given:
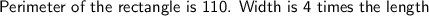
Find:
Solution: So, we are given two different statements in the problem. The first one states that the perimeter of the given rectangle is 110. We know that the perimeter formula is equal to 2(length + width). Since we know that the perimeter is equal to 110 that means that we can set the perimeter formula equal to 110.
Therefore, the first equation would be
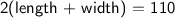 .
.
The second statement states that the width is 4 times the length. Using simple algebra we can make an equation which states that the width on one side is equal to the length multiplied by 4 on the other side.
Therefore, the second equation would be
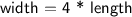 .
.
Now that we have created two equations these two would be considered as a system of equations. We can now plug in the second formula into the first one and solve for the length.
Now that we have the length, we can plug the length into the second formula and solve for the width.
In conclusion, after creating two equations and forming them into a system of equations we were able to solve for the width and determine that the value of it is 44. Therefore, the option that matches our answer would be
 .
.