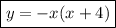Answer:
1.
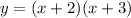
2.
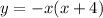
Explanation:
We can find the factored form of the graphed quadratic functions by:
1) Expressing each one in vertex form
2) Expanding and refactoring to rewrite in factored form
1. We know that vertex form is:
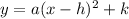 ,
,
where
 determines the parabola's direction and width (
determines the parabola's direction and width (
 being the same as a standard parabola), and
being the same as a standard parabola), and
 is the parabola's vertex.
is the parabola's vertex.
The vertex of this parabola is (-3, -4).
↓ plugging these values into the vertex form equation
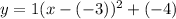
↓ simplifying
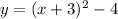
Now, we can expand and refactor this equation into factored form.
↓ expanding the squared term
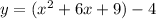
↓ simplifying
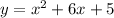
↓ factoring
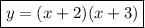
2. We can see that the vertex is at (-2, 4).
↓ plugging into the vertex form equation
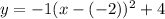
Note that the parabola opens downward, so
 .
.
↓ simplifying
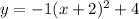
↓ expanding the squared term

↓ incorporating the outer +4 into the distribution of -1
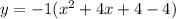
↓ simplifying
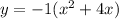
↓ factoring
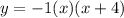
↓ simplifying