Answer:
- Infinitely many solutions.
Explanation:
To find:-
- The correct option from the given ones .
Answer:-
We are here given that there are two linear equations, namely,
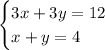
These can be rewritten as ,
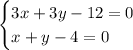
Before we precede we must know that,
Conditions for solvability :-
If there are two linear equations namely,
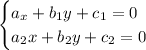
Then ,
Case 1 :-
If we have,
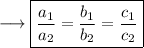
Then , the lines are coincident and there are infinitely many solutions .
Case 2 :-
If we have,

Then, the linear equations are inconsistent and have no solutions , thus the lines are parallel .

So here with respect to angle standard form of pair linear equations, we have;
Hence here we have,
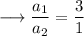
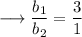
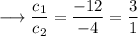
Therefore we can clearly see that,
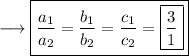
Hence there are infinitely many solutions and the lines are coincident .