Question

Find the eqn of a line segment parallel to x-3y=4 and passing through the centroid of the ∆ABC where A(3,-4) ,B(-2,1), and C(5,0)​

Answer 1

• 
  `x - 3y - 5 = 0`

Explanation:

To find:-

• The equation of the line parallel to the given line and passing through the centroid of the given traingle.

Answer:-

The given coordinates of the triangle are , A(3,-4) ; B(-2,1) and C(5,0) .

To find out the coordinate of the centroid we can use the below formula ,

`\longrightarrow \boxed{\rm{Centroid\ (G)}= \bigg((x_1+x_2+x_3)/(3),(y_1+y_2+y_3)/(3)\bigg)} \\`

where ,

• 
  `(x_1,y_1)` ;
  `(x_2,y_2)` and
  `(x_3,y_3)` are the coordinates of the triangle.

On substituting the respective values, we have;

`\longrightarrow G =\bigg((3-2+5)/(3),(-4+1+0)/(3)\bigg) \\`

`\longrightarrow G =\bigg(( 6)/(3),(-3)/(3)\bigg) \\`

`\longrightarrow \boldsymbol{ G = (2,-1) }\\`

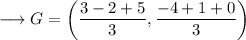
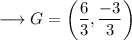
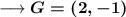
Hence the centroid of the given triangle is (2,-1) .

Now the given equation of the line is,

`\longrightarrow x - 3y = 4 \\`

Convert this into slope intercept form of the line, which is,

Slope intercept form:-

`\longrightarrow y = mx + c\\`

where, m is the slope of the line and c is the y-intercept .

So , we have;

`\longrightarrow -3y = 4-x\\`

`\longrightarrow 3y = x - 4 \\`

`\longrightarrow y =(x-4)/(3) \\`

`\longrightarrow y =(1)/(3)x-(4)/(3) \\`

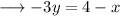
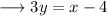
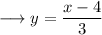
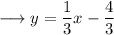
On comparing it with the slope intercept form, we have;

`\longrightarrow m =(1)/(3)\\`

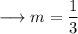
Secondly we know that the slopes of parallel lines are equal . So the slope of the line parallel to the given line would also be ⅓ .

Now we may use point slope form of the line to find out the equation of the required line. The point slope form of the line is,

Point slope form:-

`\longrightarrow y - y_1 = m(x-x_1) \\`

where the symbols have their usual meaning.

Here the line will pass through the centroid of the triangle which is (2,-1) .

On substituting the respective values, we have;

`\longrightarrow y - (-1) =(1)/(3)(x-2) \\`

`\longrightarrow 3( y +1) = x - 2 \\`

`\longrightarrow 3y + 3 = x -2\\`

`\longrightarrow x - 2 - 3 - 3y = 0 \\`

`\longrightarrow\boxed{\boldsymbol{ x - 3y - 5 =0}} \\`

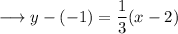
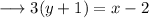
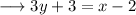
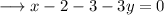
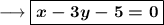
This is the required equation of the line.