Question

Find the value of q which will make the quadratic expression 9x ^2-12x+q a perfect square ​

Answer 1

The value of q that makes the expression a perfect square is q = 4.

Explanation:

Perfect square:

A perfect square expression has the following format:

`(a - b)^2 = a^2 - 2ab + b^2`

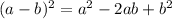
In this question:

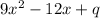`9x^2 - 12x + q` is a perfect square, we have to find the value of q.

First we have to find the value of a, looking at the equivalent formula above. So

`a^2 = 9x^2`

`a = √(9x^2)`

`a = 3x`

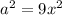
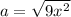
Since the second term, which is -2ab, is -12x, we have that:

`-2ab = -12x`

`-2(3x)b = -12x`

`-6xb = -12x`

`6b = 12`

`b = (12)/(6)`

`b = 2`

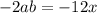
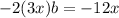
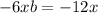
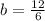
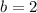
q is b squared. So

`q = b^2 = 2^2 = 4`

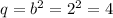
The value of q that makes the expression a perfect square is q = 4.