Question

Does this diverge or converge?

Answer 1

L = 7/6 , and the correct option is B, the series diverges.

Explanation:

Here we have that:

`an = ((3n + 3)*7^n)/(6^(n+4))`

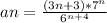
Now we want to see the quotient test, then we need to do find the value of the quotient as n tends to infinity. Then we first need to find the quotient:

`a(n + 1)/a(n) = ((3(n + 1) + 3)*7^(n + 1))/(6^(n + 1 + 4))*(6^(n + 4))/((3*(n) + 3)*7^(n))`

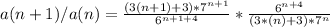
We can simplify the right part to get:

`((3(n + 1) + 3)*7^(n + 1))/(6^(n + 1 + 4))*(6^(n + 4))/((3*(n) + 3)*7^(n))= ((3n + 3 + 3)*7^(n + 1))/(6^(n + 5))*(6^(n + 4))/((3*n + 3)*7^(n))`

`((3n + 3 + 3)*7^(n + 1))/(6^(n + 5))*(6^(n + 4))/((3*n + 3)*7^(n))= ((3n + 3 + 3)*7)/((3*n + 3)*6)`

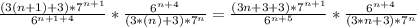
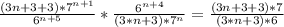
Now we want to find the limit of this as n goes to infinity, we can see that both parts will tend to infinity, then we need to use the Lhopital rule and find the limit of the quotient of the first derivatives.

The first derivatives are:

For the denominator: (3*6)

For the numerator: (3*7)

Then we need to find the limit as n goes to infinity to:

`(3*7)/(3*6) = (7)/(6)`

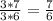
But this does not depend on the value of n, then the limit is just 6/7.

L = 7/6

And 7/6 > 1.

Then we can conclude that our series diverges.