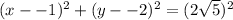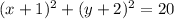Answer:
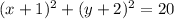
Explanation:
Using the mid point formula to find the center of the circle:
midpoint =
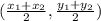
Midpoint =

Midpoint =
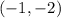
The midpoint is the same as the centre of the circle
Find the distance(the diameter of the circle) between those two points to find the radius:
Distance formula =
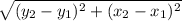
Distance formula =
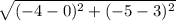
Distance formula =

Distance formula =
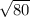
So,the diameter is
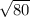 and to find the radius we need to divide the diameter by two
and to find the radius we need to divide the diameter by two
Radius =
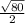
Radius =
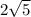
the equation of circle:
Radius =
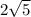
Center = (-1,-2)