Question

a walking path BE in a park intersects intersects two sides of the park at their midpoints. You walk from point D to E, E to B, from B to C, and back to point D. How many yards did you walk?

Answer 1

456

Explanation:

107

74

254/2 =127

74x2=148

107+74+127+148=456

Answer 2

Total distance covered = 436 yards

Explanation:

Walking path BE joins the midpoints B and E of the sides AC and AD.

By midsegment theorem,

"Line joining midpoints of two sides of a triangle is parallel and measure half of the third side"

m(BE) =
`(1)/(2)[m(CD)]`

CD = 2(BE)

CD = 2(74) = 128 yd

From starting point D,

DE = 107 yd

EB = 74 yd

BC =
`(254)/(2)`

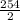
= 127 yd

CD = 128 yd

Total walking distance = DE + EB + BC + CD

= 107 + 74 + 127 + 128

= 436 yd

Total distance covered = 436 yards