Question

a 1300-kg car moving on a horizontal surface has speed v = 65 km/h when it strikes a horizontal coiled spring and is brought to rest in a distance of 2.1 m. What is the spring stiffness constant of the spring? Express your answer using two significant figures.

Answer 1

Approximately
`9.7* 10^(6)\; {\rm N\cdot m^(-1)}`.

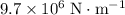Step-by-step explanation:

Apply unit conversion and ensure that the initial speed of the vehicle is in the standard unit of meters per second:

`\begin{aligned}v &= 65\; {\rm km\cdot h^(-1)}\, \frac{1\; {\rm h}}{3600\; {\rm s}}\cdot \frac{1000\; {\rm m}}{1\; {\rm km}} \\ &\approx 18.1\; {\rm m\cdot s^(-1)} \end{aligned}`.

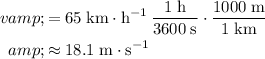Before hitting the spring, the kinetic energy (
`\text{KE}`) of this vehicle would be:

`\begin{aligned} (\text{KE}) = (1)/(2)\, m\, v^(2) \end{aligned}`,

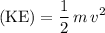Where:

• 
  `m = 1300\; {\rm kg}` is the mass of the vehicle, and
• 
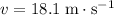  `v = 18.1\; {\rm m\cdot s^(-1)}` is the speed of the vehicle.

Let
`k` denote the spring constant. When the spring is compressed by
`x` from equilibrium, the elastic potential energy (
`\text{EPE}`) in the spring would be:

`\displaystyle (\text{EPE}) = (1)/(2)\, k\, x^(2)`.

Assuming that the kinetic energy of the vehicle was entirely turned into the elastic potential energy in the spring:

`(\text{loss in KE}) = (\text{gain in EPE})`.

`\begin{aligned}(1)/(2)\, m\, v^(2) &= (1)/(2)\, k\, x^(2)\end{aligned}`.

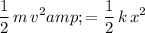Rearrange this equation to find the spring constant
`k`:

`\begin{aligned}k &= (m\, v^(2))/(x^(2)) \\ &\approx ((1300)\, (18.1)^(2))/((2.1)^(2))\; {\rm N\cdot m^(-1)} \\ &\approx 9.7* 10^(6)\; {\rm N\cdot m^(-1)} \end{aligned}`.