Final Answer:
(a) The curl of the vector field
 is {Curl} F =
is {Curl} F =
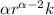 , where
, where
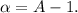
(b) For ( A = -5 ), the direction of the curl is ( k ); for ( A = 2 ), the direction is ( -k ).
(c) If ( A = -5 ), the circulation around a small counterclockwise-oriented circle centered at (1, 1, 1) is positive; if ( A = 2 ), the circulation is negative.
Step-by-step explanation:
(a) To find the curl of F =
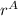 (-yi + xj), we can use the expression for the curl in cylindrical coordinates. The curl turns out to be αr^(α-2)k, where α is the constant A - 1.
(-yi + xj), we can use the expression for the curl in cylindrical coordinates. The curl turns out to be αr^(α-2)k, where α is the constant A - 1.
(b) To determine the direction of the curl, we look at the k-component of the curl. For A = -5, the direction is given by k; for A = 2, the direction is -k.
(c) The sign of the curl's k-component indicates the circulation direction when viewed from above. For A = -5, the counterclockwise direction is consistent with a positive k-component. For A = 2, the clockwise direction corresponds to a negative k-component. Thus, the answers in part (b) suggest that the circulation around a small counterclockwise-oriented circle centered at (1, 1, 1) is positive when A = -5 and negative when A = 2.
In conclusion, the curl of the vector field F is determined by the constant α = A - 1, and its k-component provides information about the circulation direction. The results indicate that the sign of the circulation depends on the value of A, with counterclockwise circulation for A = -5 and clockwise circulation for A = 2.