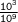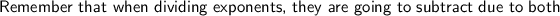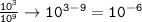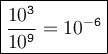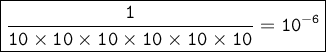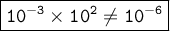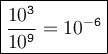Question

Negative Exponent Rule: Which expressions are equivalent to 10−6? Select all that apply.

Answer 1

`\large\boxed{\textsf{See Below.}}`

Explanation:

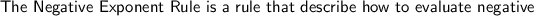
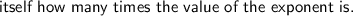
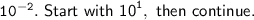
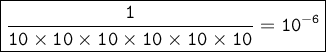
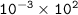
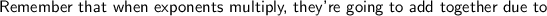
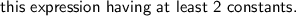
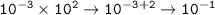
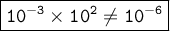
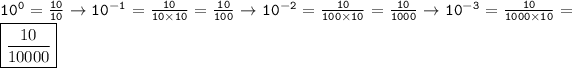
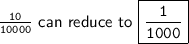
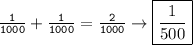
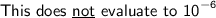
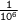
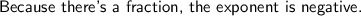
`\textsf{We are asked which expressions are equivalent to 10}^(\tt -6).`

`\textsf{We are given that we need to use the \underline{Negative Exponent Rule}.}`

`\large\underline{\textsf{What is the Negative Exponent Rule?}}`

`\textsf{The Negative Exponent Rule is a rule that describe how to evaluate negative}`

`\textsf{exponents.}`

`\large\underline{\textsf{How do we use the Negative Exponent Rule?}}`

`\textsf{We use the negative exponent rule to multiply the denominator of a number by}`

`\textsf{itself how many times the value of the exponent is.}`

`\underline{\textsf{Example of the Negative Exponent Rule;}}`

`\tt 10^(-2). \ \textsf{Start with 10}^(\tt 1), \ \textsf{then continue.}`

`\tt 10^(1) = (10)/(1) \rightarrow 10^(\tt 0) = (10)/(1 * 10) = (10)/(10) \rightarrow 10^(\tt -1) = (10)/(10 * 10) = (10)/(100) \rightarrow 10^(\tt -2) = (10)/(100 * 10) = \boxed{ (10)/(1000) }`

`\large\underline{\textsf{Use the Negative Exponent Rule for our given expressions;}}`

`\tt (1)/(10 * 10 * 10 * 10 * 10 * 10) \overset{\textsf{is the same as}} \rightarrow (1)/(10^(6))`

`\textsf{There is a fraction for this expression, meaning that the exponent is negative.}`

`\tt (1)/(10^(6)) = 10^(\tt -6)`

`\large\boxed{\tt (1)/(10 * 10 * 10 * 10 * 10 * 10) = 10^(\tt -6)}`

-------------------------------------------------------------------------

`\tt 10^(\tt -3) * 10^(\tt 2)`

`\textsf{Remember that when exponents multiply, they're going to add together due to}`

`\textsf{this expression having at least 2 constants.}`

`\tt 10^(\tt -3) * 10^(\tt 2) \rightarrow 10^(\tt -3+2) \rightarrow 10^(\tt -1)`

`\large\boxed{\tt 10^(\tt -3) * 10^(\tt 2) \\eq 10^(\tt -6)}`

-------------------------------------------------------------------------

`\tt 10^(\tt -3) + 10^(\tt -3)`

`\textsf{We should know that adding exponents is not like adding whole numbers/terms.}`

`\textsf{We will need to evaluate 10}^(\tt -3) \ \textsf{using the Negative Exponent Rule.}`

`\tt 10^(\tt 0) = (10)/(10) \rightarrow \tt 10^(\tt -1) = (10)/(10 * 10) = (10)/(100) \rightarrow \tt 10^(\tt -2) = (10)/(100 * 10) = (10)/(1000) \rightarrow \tt 10^(\tt -3) = (10)/(1000 * 10) = \boxed{(10)/(10000)}`

`\tt (10)/(10000) \ \textsf{can reduce to} \ \boxed{\tt (1)/(1000)}`

`\underline{\textsf{We are now adding;}}`

`\tt (1)/(1000) + (1)/(1000) = (2)/(1000) \rightarrow \boxed{(1)/(500) }`

`\textsf{This does \underline{not} evaluate to 10}^(\tt -6)`

`\large\boxed{\tt 10^(\tt -3) + 10^(\tt -3) \\eq 10^(\tt -6)}`

-------------------------------------------------------------------------

`\tt (1)/(10^(\tt 6))`

`\textsf{Because there's a fraction, the exponent is negative.}`

`\large\boxed{\tt (1)/(10^(\tt 6)) = 10^(\tt -6)}`

-------------------------------------------------------------------------

`\tt (10^(\tt 3))/(10^(\tt 9))`

`\textsf{Remember that when dividing exponents, they are going to subtract due to both}`

`\textsf{of these numbers are constants.}`

`\tt (10^(\tt 3))/(10^(\tt 9)) \rightarrow \tt 10^(\tt 3-9) = 10^(\tt -6)`

`\large\boxed{(10^(\tt 3))/(10^(\tt 9)) = 10^(\tt -6)}`

`\large\underline{\textsf{Hence;}}`

`\large\boxed{\tt (1)/(10 * 10 * 10 * 10 * 10 * 10) = 10^(\tt -6)}`

`\large\boxed{\tt 10^(\tt -3) * 10^(\tt 2) \\eq 10^(\tt -6)}`

`\large\boxed{\tt 10^(\tt -3) + 10^(\tt -3) \\eq 10^(\tt -6)}`

`\large\boxed{\tt (1)/(10^(\tt 6)) = 10^(\tt -6)}`

`\large\boxed{(10^(\tt 3))/(10^(\tt 9)) = 10^(\tt -6)}`