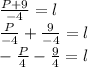Question

Solve for the indicated variable in the literal equation. REAL ANSWERS ONLY!​

Answer 1

`\large \boxed{l = (P + 9)/( - 4) }`

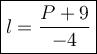
See below for two alternative solutions.

Explanation:

Goal

• Solve for the l-term.

Given Equation

• 
  `P = - 3 - 4l - 6`

Step 1

• Make the l-term as the subject of equation by moving - 3 and - 6 to another side so we can leave l-term as the subject.

`P + 3 + 6 = - 4l`

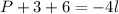
Simplify by adding 3 and 6.

`P + 9 = - 4l`

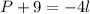
Remember that we cannot combine a variable and a constant. We can only combine a like term.

Step 2

• Move -4 to divide P+9 so we can finally solve for l-term.

`(P + 9)/( - 4) = l`

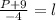
Alternative Solutions

• 1) We change the position of the negative sign of 4.

`- (P - 9)/(4) = l`

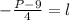
• 2) Simplify in the simplest form.

`(P + 9)/( - 4) = l \\ (P)/( - 4) + (9)/( - 4) = l \\ - (P)/(4) - (9)/(4) = l`