Question

A toy rocket is launched vertically upward from ground level with an initial velocity of 128 feet per second, then its height h after t seconds, is given by the equation h(t)=-16t^2+128 if air resistance is neglected

1. how high is the rocket off the ground when it’s launched ?
2. What time does the maximum height occur?
3. How high does the rocket go?
4. What is the axis of symmetry?
5. When does the rocket hit the ground?
6. How high is the rocket at 2 seconds?
7. When is the rocket at 252 feet?
8. The graph coordinates

Answer 1

1. The rocket is off the ground by 0 feet when it's launched, as ground level is defined as h = 0.
2. To find the time at which the maximum height occurs, we can use the fact that the maximum or minimum point of a parabola given in the form y = ax^2 + bx + c occurs at x = -b/2a. In this case, we have h(t) = -16t^2 + 128, which has a = -16 and b = 0. Therefore, the maximum height occurs at t = -b/2a = -0/(-32) = 0 seconds.
3. To find the maximum height reached by the rocket, we can substitute t = 0 into the equation h(t) = -16t^2 + 128, since the maximum height occurs at t = 0:

`h(0) = -16(0)^2 + 128`

`= 128`

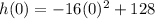
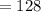
Therefore, the rocket goes to a maximum height of 128 feet.

4. The axis of symmetry of the parabolic path of the rocket is the vertical line that passes through the vertex of the parabola. Since the coefficient of
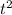`t^2` is negative, the parabola opens downwards, and the vertex represents the maximum point of the path. As we found in question 2, the time at which the maximum height occurs is t = 0, so the axis of symmetry is the vertical line passing through t = 0.

5. To find when the rocket hits the ground, we need to find the time t at which h(t) = 0. Substituting
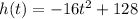`h(t) = -16t^2 + 128`, we get:

`-16t^2 + 128 = 0`

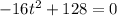
Solving for t using the quadratic formula, we get:

t = (0 ± √(0^2 - 4(-16)(128))) / (2(-16))

= (±√8192) / (-32)

= ±8

Since time cannot be negative, the rocket hits the ground after approximately 8 seconds.

6. To find how high the rocket is at t = 2 seconds, we can substitute t = 2 into the equation h(t) = -16t^2 + 128:

h(2) = -16(2)^2 + 128

= -64 + 128

= 64 feet

Therefore, the rocket is at a height of 64 feet at 2 seconds.

7. To find when the rocket is at a height of 252 feet, we need to solve the equation
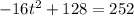`-16t^2 + 128 = 252`. Rearranging and solving for t, we get:

`-16t^2 + 128 = 252`

`-16t^2 = 124`

`t^2 = -124/-16`

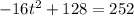
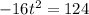
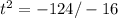
t^2 = 7.75

t ≈ ±2.78 seconds

Since time cannot be negative, the rocket is at a height of 252 feet after approximately 2.78 seconds.

8. The graph coordinates of the rocket's path can be plotted using the function
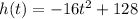`h(t) = -16t^2 + 128`. The x-axis represents time t in seconds and the y-axis represents the height of the rocket in feet. We can plot points on the graph by substituting different values of t into the equation and plotting the resulting height. For example, some common points to plot include the vertex at (0, 128), the point where the rocket hits the ground at approximately (8, 0), and the point where the rocket is at a height of 252 feet at approximately (2.78, 252). We can also plot other points by substituting different values of t into the equation and plotting the resulting height.

Answer 2

1. The rocket is at a height of 0 feet off the ground when it is launched.
2. The maximum height occurs at the vertex of the parabolic curve. To find the time, we need to find the t-value that corresponds to the axis of symmetry. The axis of symmetry is given by the formula t = -b/2a, where a = -16 and b = 0. Plugging in these values, we get t = 0 seconds. Therefore, the maximum height occurs at t = 0 seconds.
3. To find the maximum height, we need to evaluate the equation at the time of the maximum height. We know from part 2 that the maximum height occurs at t = 0 seconds. Plugging in t = 0 into the equation, we get h(0) = -16(0)^2 + 128 = 128 feet. Therefore, the rocket goes up to a height of 128 feet.
4. The axis of symmetry is given by the formula t = -b/2a, where a = -16 and b = 0. Plugging in these values, we get t = 0 seconds. Therefore, the axis of symmetry is the vertical line passing through the point (0, 0).
5. To find when the rocket hits the ground, we need to find the time when the height is 0. Setting h(t) = 0 and solving for t, we get -16t^2 + 128 = 0, which simplifies to t^2 = 8. Solving for t, we get t = ±√8. Since we are only interested in the positive value, t = √8 seconds. Therefore, the rocket hits the ground at approximately 2.83 seconds after it is launched.
6. To find the height of the rocket at 2 seconds, we need to evaluate the equation at t = 2 seconds. Plugging in t = 2 into the equation, we get h(2) = -16(2)^2 + 128 = 96 feet. Therefore, the rocket is at a height of 96 feet at 2 seconds after it is launched.
7. To find when the rocket is at a height of 252 feet, we need to solve the equation h(t) = 252 for t. Substituting h(t) = -16t^2 + 128, we get -16t^2 + 128 = 252, which simplifies to -16t^2 = -124. Solving for t, we get t = √(124/16) seconds. Therefore, the rocket is at a height of 252 feet at approximately 2.79 seconds after it is launched.
8. The graph coordinates are (0, 128) for the vertex, (2, 96) for a point on the curve, and (√8, 0) for the point where the rocket hits the ground.