Question

6. Two triangular planters sit in the rose

garden. Excluding the planters, how many
square feet of garden area remain?
14 ft
5 ft
5 ft
5 ft
T
4 ft 5 ft
30 ft
5 ft N
5 ft
5 ft

Answer 1

• 
  `\rm Area = 400 \ ft^2 \\`

Explanation:

To find:-

• Area excluding the planters .

Answer:-

We can see that the two triangular planters are inside a rectangular area of dimensions 14ft*30ft .

To find out the area excluding the triangle, we need to subtract the area of two triangles from the rectangle.

So , we know that,

Area of the rectangle:-

• 
  `\longrightarrow A = \ell b \\`

Where "l" is the length of the rectangle and "b" is the breadth.

Area of triangle :-

• 
  `\longrightarrow A =(bh)/(2) \\`

where "b" is the base of the triangle and "h" is the height.

So we can calculate the required area as ,

`\longrightarrow \rm A = A_(rectangle)-A_(2 \ triangles) \\`

`\longrightarrow \rm A = 14(30) - 2\left( (4(5))/(2)\right) \\`

`\longrightarrow \rm A = 420 - 20 \\`

`\longrightarrow \rm \bf A = 400 \ ft^2 \\`

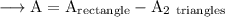
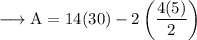
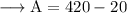
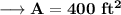
Hence the area of the rectangle without the planters is 400 ft.² .