Question

Can someone help me fast!?!?

Trying to get better at doing word problems like this is would help a lot.

The linear function f(x) = 0.4x + 81 represents the average test score in your language arts class, where x is the number of the test taken. The linear function g(x) represents the average test score in your social studies class, where x is the number of the test taken.

First part: Determine the test average for your language arts class after completing test 2.
Second part: Determine the test average for your social studies class after completing test 2.
Third part: Which class had a higher average after completing test 4? Show work to support your answer.

Answer 1

1st: 81.8

2nd: 82

3rd: Language arts class

Explanation:

1st: We're told that f(x) = 0.4x + 81 represents the avg. test score in your language arts class, where x is the number of the test taken. We know then that f(x) is the average test score. Thus, to find the average test score for test 2, we plug in 2 for x into the function:

f(2) = 0.4(2) + 81

f(2) = 0.8 + 81

f(2) = 81.8

2nd: Although we're not given the formula for g(x), we know that it is linear and have enough information to find the formula.

The general form for a linear formula is y = mx + b, where m is the slope (change in y / change in x) and b is the y-intercept (point for y when x = 0)

We can find the slope using the slope formula, which is:

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) )`

We can use any two consecutive points to find the slope:

*Note that y is synonymous with g(x)

Thus, if we allow (1, 84) to represent x1 and y1 and (2, 82) to represent x2 and y2, our slope is:

`m=(82-84)/(2-1)\\ m=-2`

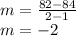
Now, we can choose any point like (1, 84) and plug in the point and the slope we've found to find b or our y-intercept:

`84=-2(1)+b\\84=-2+b\\86=b`

Thus, the formula for g(x) is g(x) = -2x + 86.

Like we did for f(x), we can simply plug in 2 for x to find the average test score for test 2 in your social studies class:

g(2) = -2(2) + 86

g(2) = -4 + 86

g(2) = 82

Third: To find which class had a higher average after completing test 4, we plug in 4 into each function:

f(4) = 0.4(4) + 81

f(4) = 1.6 + 81

f(4) = 82.6

g(4) = -2(4) + 86

g(4) = -8 + 86

g(4) = 78

Therefore, the language arts class had a higher average score for test 4 than the social studies class.