Question

(5,2) A line that passes through each given point and is parallel to y= -3x + 8

Answer 1

• 
  `y = - 3x + 17`

Explanation:

To find:-

• The equation of the line passing through (5,2) and parallel to
  `y = -3x+8`

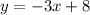
Answer:-

We are interested in finding out the equation of the line which is parallel to the given line. The equation of the given line is,

`\longrightarrow y = -3x + 8 \\`

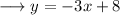
The given line is in slope intercept form, the slope intercept form of the line is,

Slope intercept form :-

`\longrightarrow \boxed{\boldsymbol{ y = mx + c }} \\`

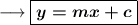
where ,

• 
  `m` is the slope .
• 
  `c` is the y-intercept .

On comparing, we have,

`\longrightarrow y =\boxed{-3}x+8 \\`

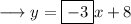
The slope is ,

`\longrightarrow m = -3 \\`

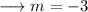
Now as , we know that the slopes of parallel lines are equal . Hence the slope of the line parallel to the given line, would be -3 . The given point to us is (5,2) ; so we can use the point slope form of the line to find out the equation. The point slope form of the line is,

Point slope form:-

`\longrightarrow y - y_1 = m(x-x_1) \\`

where ,

• 
  `m` is the slope .
• 
  `(x_1,y_1)` is the coordinate through which the line passes.

On substituting the respective values, we have;

`\longrightarrow y - 2 = -3(x-5) \\`

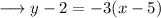
Simplify by opening the brackets , as ;

`\longrightarrow y - 2 = -3x + 15\\`

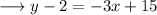
Add "2" on both the sides,

`\longrightarrow y = -3x+15+2 \\`

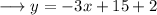
Add the constant terms ,

`\longrightarrow \boxed{\boldsymbol{ y = -3x+17}}\\`

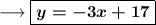
This is the required equation of the line.