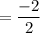The slope of the first line is 0, as per slope-intercept form.
What is the slope of a straight line?
The linear equation
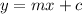 represents the slope-intercept form of a line passing through the point
represents the slope-intercept form of a line passing through the point
 .
.
Here, 'm' is the slope and 'c' is the y-intercept of the given line.
The slope of a line that passes through points
 and
and
 is defined as:
is defined as:
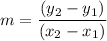
Here, the slope of the first line that passes through
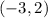 and
and
 is
is
![= ((2-2))/([- 1 - (- 3)])](https://img.qammunity.org/2024/formulas/mathematics/high-school/2o05eqb9gm2ipzoptuldtmtiuyn3rc07fy.png)
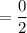

Now, the slope of the second line that passes through
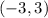 and
and
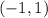 is
is
![=((1-3))/([- 1 - (- 3)])](https://img.qammunity.org/2024/formulas/mathematics/high-school/mgmwohkyyfmebgvyy5hp1wqkclypyvpkdu.png)