Question

A 1.3 kg cart rests on an inclined plane. The cart is released so that it is free to roll down the frictionless surface. The inclined plane is

tilted by 14°. Find the acceleration of the cart.

(1) 9.5 m/s²

(2) 9.8 m/s²

(3) 2.3 m/s²

(4) 3.1 m/s²

Answer 1

The third option

2.3 m/s²

Step-by-step explanation:

We can use Newton's Second Law to evaluate the acceleration.

Newton's Second Law of states that the acceleration of an object is directly proportional to the force applied to the object and inversely proportional to its mass.

Mathematically, it can be written as

`\sf F_(net) =ma`

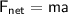
In the absence of friction and drag on an inclined plane we have 2 main forces acting on the object.

1. Weight force
`\sf F_w`: This is the force exerted by the gravitational attraction of the Earth on the object. The weight force always acts vertically downwards.

`\sf F_W=mg\sin \theta`

2. Normal force
`\sf F_N`: This is the force exerted by the inclined plane on the object perpendicular to the plane. It counteracts the weight force and prevents the object from sinking into the plane. The normal force always acts perpendicular to the plane.

`\sf F_N=mg\cos \theta`

Therefore, neglecting friction and drag, the net force acting on the object will be:

`\sf F_(net) =mg\sin \theta`

`\boxed{\sf ma=mg\sin \theta}`

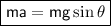
Numerical Evaluation

In this example we are given

`\sf m=1.3\\\sf g=9.81\\\sf \theta =14`

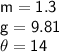
First we can cancel out the common term
`\sf m` in your equation which leaves us with

`\sf a=g\sin \theta`

Substituting our given values into the equation yields

`\sf a=9.81\sin 14`

`\sf a=2.37325379`

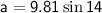
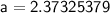
Rounding to the nearest tenth leaves us with

`\sf a=2.4`

The closest answer choice given is 2.3 m/s²