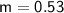Answer:
The mass of the object is 0.53 kg.
Step-by-step explanation:
We can use the internal energy of an ideal gas equation do evaluate the mass.

Where
 is the change in internal energy
is the change in internal energy
 is the mass of the object
is the mass of the object
 is the specific heat capacity of the object
is the specific heat capacity of the object
 is the change in temperature
is the change in temperature
We can rearrange the equation to isolate the mass (
 ).
).
Divide both sides of the equation by
 .
.
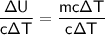
 cancels out on the right side leaving us with
cancels out on the right side leaving us with

Numerical Evaluation
In this example we are given
 J
J
 J/°C/kg
J/°C/kg
 °C
°C
Substituting our given values into the equation yields
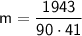

Rounding to 2 decimal places leaves us with