Question

ms tilly garden has an area of 28 1/4 square yards the width of the garden is 2 1/2 yards what is the length in yards of ms tillys garden

Answer 1

• length = 11³/₁₀ yards .

Explanation:

To find:-

• The length of the garden in yards.

Answer:-

We are here given that the area of MsTilly's garden is 28¼ yards² and the width of the garden is 2½ yards. We are interested in finding out the length of the graden.

Since the garden is rectangle, we can find out it's area as ,

→ Area = length*width

On substituting the respective values, we have;

→ 28¼ = l * 2½

Convert the given mixed fractions into improper fractions as ,

→ 113/4 = l * 5/2

Divide both the sides by 5/2 as ,

→ 113/4 ÷ 5/2 = l

Simplify,

→ 113/4 * 2/5 = l

→ l = 113/10

Convert the improper fraction into mixed fraction as ,

→ l = 11³/₁₀ yards

Hence the length of the garden is 11³/₁₀ yards .

Answer 2

The length of Ms Tilly's garden is 11 ³/₁₀ yards.

Explanation:

We can model Ms Tilly's garden as a rectangle.

The area of a rectangle is the product of its width and length:

`\boxed{\sf Area\;of\;a\;rectangle=width * length}`

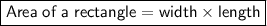
Given that the area of the garden is 28 ¹/₄ square yards and its width is 2 ¹/₂ yards, we can substitute these values into the formula and solve for length to find the length of her garden.

As the values are mixed numbers, begin by converting them into improper fractions.

To convert a mixed number into an improper fraction, multiply the whole number by the denominator of the fraction, add this to the numerator of the fraction, and place the answer over the denominator:

`\implies 28 (1)/(4)=(28 * 4+1)/(4)=(113)/(4)`

`\implies 2 (1)/(2)=(2 * 2+1)/(2)=(5)/(2)`

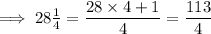
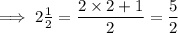
Now substitute the values into the area formula:

`\begin{aligned} \textsf{Area of the garden}&=\sf width * length\\\\\implies (113)/(4)&=(5)/(2) * \sf length\end{aligned}`

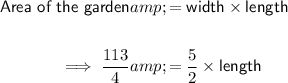
To solve the equation for length, divide both sides by ⁵/₂.

Remember that dividing by a fraction is the same as multiplying by the reciprocal of that fraction. Therefore, we can multiply both sides of the equation by ²/₅:

`\begin{aligned} \textsf{Area of the garden}&=\sf width * length\\\\\implies (113)/(4)&=(5)/(2) * \sf length\\\\\implies (2)/(5) * (113)/(4)&=(2)/(5) *(5)/(2) *\sf length\\\\\implies (2 * 113)/(5 * 4)&=\sf length\\\\\implies \textsf{length}&=(226)/(20)\\\\\implies \textsf{length}&=(226/2)/(20/2)\\\\\implies \textsf{length}&=(113)/(10)\end{aligned}`

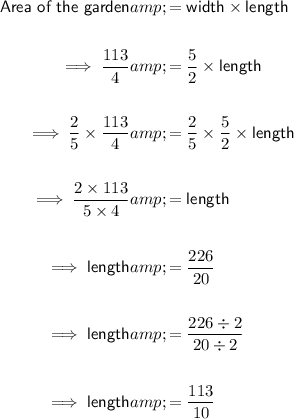
Finally, convert the improper fraction back into a mixed number by dividing the numerator by the denominator:

`\implies 113 / 10=11\;\rm remainder\;3`

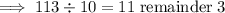
The mixed number answer is the whole number and the remainder divided by the denominator:

`\implies (113)/(10)=11 (3)/(10)`

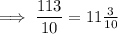
Therefore, the length of Ms Tilly's garden is 11 ³/₁₀ yards.