Question

HELPPPPPPPPPPPPPPPPPPPPPPPPPP

Answer 1

○=> Solution (7) :

A given set of data is said to have a greater spread if it covers a large scale/area. Since the data set 3 only covers a small portion of a wide spectrum it is said to have a smaller spread when in comparison with data set 4 which has a greater spread as it covers a larger scale/spectrum.

▪︎Therefore, Data set 4 has a greater spread.

○=> Solution (8) :

Lower quartile of a data set is said to be the median of the lower half of the data set.

Lower quartile of this data set :

`= \tt (50 + 60)/(2)`

`=\tt (110)/(2)`

`\color{plum} =\tt 55`

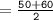
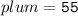
Thus, the lower quartile of this data set = 55

Median is said to be the middle element of a data set.

The median of this data set = 80

Upper quartile of a data set is said to be the median of the upper half of a given data set.

Upper quartile of this data set :

`=\tt (110 + 100)/(2)`

`=\tt (210)/(2)`

`\color{plum} = \tt105`

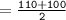
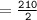
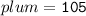
Thus, the upper quartile of this data set = 105

Therefore :

▪︎Lower quartile of this data set = 55

▪︎Upper quartile of this data set = 105

▪︎Median of this data set = 80