Question

Find all solutions to the equation x3 – 4x2 + 9x – 10 = 0.

Answer 1

The solutions to the equation x³ - 4x² + 9x - 10 = 0 are x = 1 + 2i, x = 1 - 2i and x = 2

How to determine the solutions to the equation

From the question, we have the following parameters that can be used in our computation:

x³ - 4x² + 9x - 10 = 0

Using the remainder theroem, we set x = 2 to test if x - 2 is a factor

So, we have

2³ - 4(2)² + 9(2) - 10 = 0

0 = 0

So, x - 2 is a factor

Using the long division method of quotient, we have

x² - 2x + 5

x - 2 | x³ - 4x² + 9x - 10

x³ - 2x²

-----------------------------------------

- 2x² + 9x - 10

- 2x² + 4x

-----------------------------------------

5x - 10

5x - 10

-----------------------------------------

0

So, we have

x³ - 4x² + 9x - 10 = (x² - 2x + 5)(x - 2)

This means that

x² - 2x + 5 = 0 or x - 2 = 0

x² - 2x + 5 = 0 or x = 2

Solving x² - 2x + 5 = 0 graphically, we have

`x = (-b \pm √(b^2 - 4ac))/(2a)`

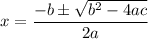
So, we have

`x = (2 \pm √((-2)^2 - 4 * 1 * 5))/(2 * 1)`

`x = (2 \pm √(-16))/(2)`

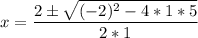
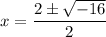
Evaluate the square root

`x = (2 \pm 4√(-1))/(2)`

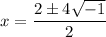
Divide

x = 1 ± 2i

Splif

x = 1 + 2i and x = 1 - 2i

Hence, the solutions to the equation are x = 1 + 2i, x = 1 - 2i and x = 2