Answer:
58.
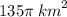
59.
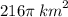
60.
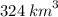
61.
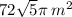
62.
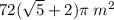
63.
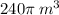
Explanation:
58. First, we have to find the length of the cone shaper by using the Pythagorean theorem:

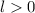

Now, let's find the lateral surface (r = 9 km):
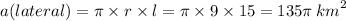
59. The area of total surface is equal to a lateral surface's and base surface's sum:
Let's find the area of the base first:
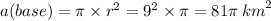
Now, let's find the area of total surface:
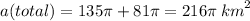
60. h = 12 km
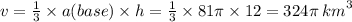
61. r = 12m
h = 5m
Let's find the length of the cone shaper by using the Pythagorean theorem:
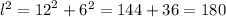
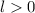
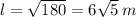
Now, let's find the area of the lateral surface:
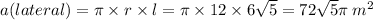
62.
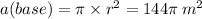
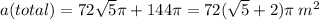
63.
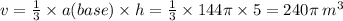
I don't know if these answer are correct, though...